Qué son las pruebas paramétricas y no paramétricas

Las pruebas estadísticas son herramientas fundamentales en la investigación científica y analítica. Nos permiten tomar decisiones informadas basadas en datos, y dentro de este ámbito, existen dos categorías principales de este tipo de pruebas: las pruebas paramétricas y las pruebas no paramétricas. Aunque ambos tipos de pruebas tienen el mismo objetivo general de analizar datos y sacar conclusiones, difieren significativamente en su aplicación, supuestos y tipos de datos a los que se dirigen. Comprender la diferencia entre estas pruebas es esencial para los investigadores y analistas que desean aplicar correctamente la metodología estadística en sus estudios.

En este artículo, exploraremos en profundidad qué son las pruebas paramétricas y las no paramétricas, destacando sus características, supuestos, y cuándo es apropiado emplearlas. Además, analizaremos ejemplos concretos de cada tipo y las consideraciones que deben tener en cuenta los investigadores al seleccionar la prueba más adecuada para sus datos y objetivos. A medida que avancemos, proporcionaremos información detallada que no solo esclarecerá estos conceptos, sino que también facilitará su aplicación práctica en trabajos de investigación y análisis de datos.

Definición de pruebas paramétricas

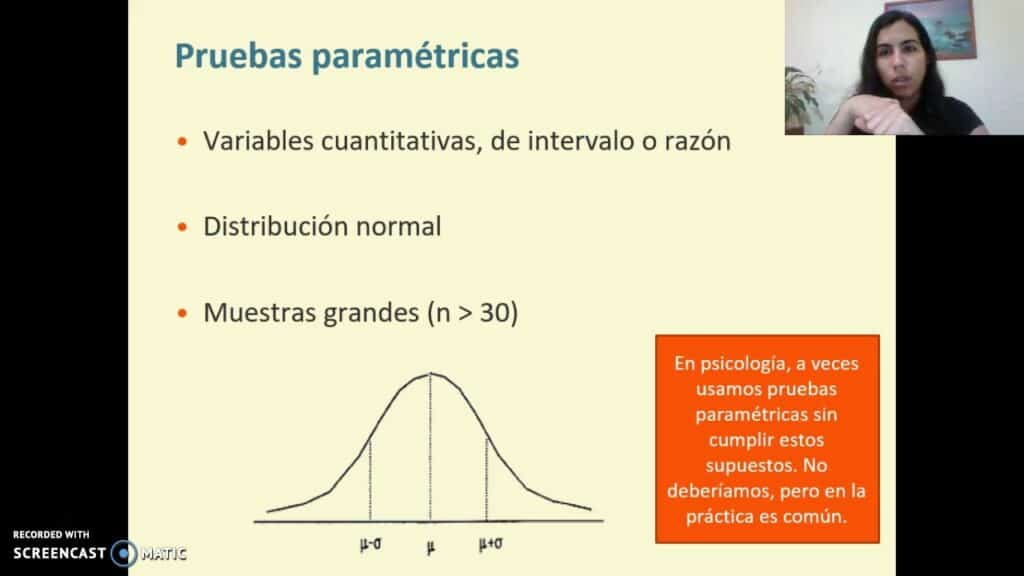
Las pruebas paramétricas son un conjunto de métodos estadísticos que se basan en supuestos específicos sobre la población de la que se extraen los datos. Principalmente, estas pruebas asumen que los datos tienen una distribución normal, lo que significa que la mayor parte de los datos se agrupan alrededor de la media, formando una curva de campana. Este tipo de pruebas también requiere que los datos sean de una escala continua y homogénea. Ejemplos comunes de pruebas paramétricas incluyen la prueba t de Student, el análisis de varianza (ANOVA) y la regresión lineal.

La clave para entender las pruebas paramétricas radica en los supuestos sobre la normalidad y la homogeneidad de las varianzas. Si estos supuestos se cumplen, las pruebas paramétricas son muy poderosas y pueden detectar diferencias significativas con un tamaño de muestra relativamente pequeño. Sin embargo, si los datos no se distribuyen normalmente, la validez de los resultados puede verse comprometida, lo que podría llevar a conclusiones erróneas. Por lo tanto, antes de aplicar una prueba paramétrica, los investigadores deben comprobar los supuestos a través de análisis exploratorios de datos, tales como histogramas y pruebas de normalidad, como la prueba de Shapiro-Wilk.

Definición de pruebas no paramétricas

Las pruebas no paramétricas, por otro lado, son herramientas estadísticas que no requieren que los datos sigan una distribución específica. Estas pruebas son útiles en situaciones donde los datos no cumplen los supuestos necesarios para las pruebas paramétricas. Además, son ideales para datos ordinales o categóricos. Ejemplos de pruebas no paramétricas incluyen la prueba de Mann-Whitney, la prueba de Kruskal-Wallis y el coeficiente de correlación de Spearman.

La principal ventaja de las pruebas no paramétricas es su flexibilidad. Dado que no dependen de supuestos estrictos sobre la distribución de los datos, pueden aplicarse a un rango más amplio de situaciones. Esto es especialmente importante en investigaciones donde los tamaños de muestra son pequeños o donde los datos presentan características no típicas. Sin embargo, es importante señalar que las pruebas no paramétricas suelen tener menos potencia estadística que sus contrapartes paramétricas, lo que significa que pueden requerir muestras más grandes para detectar diferencias significativas. A pesar de esto, son herramientas valiosas que ofrecen opciones cuando los supuestos de las pruebas paramétricas no se sostienen.

Comparación entre pruebas paramétricas y no paramétricas

Al considerar las diferencias entre las pruebas paramétricas y no paramétricas, es fundamental examinar varios factores, incluyendo sus supuestos, tipos de datos y la potencia estadística. Las pruebas paramétricas, como se mencionó anteriormente, requieren que los datos cumplan con ciertos supuestos, principalmente la normalidad y homogeneidad de varianzas. Esto limita su aplicación en algunas situaciones, mientras que las pruebas no paramétricas no imponen estas restricciones, lo que las hace más versátiles en términos de aplicación.

En cuanto a los tipos de datos que pueden analizar, las pruebas paramétricas son apropiadas para datos en intervalos o razones, mientras que las no paramétricas funcionan bien con datos nominales y ordinales. Esta diferencia es crucial en el diseño del estudio y el análisis de datos. Además, como se destacó, las pruebas paramétricas suelen ser más potentes, lo que significa que, bajo condiciones adecuadas, tienen una mayor probabilidad de detectar diferencias cuando realmente existen.

Aplicación de pruebas paramétricas y no paramétricas

La aplicación de pruebas paramétricas y no paramétricas en la investigación debe basarse en el tipo de datos, el tamaño de la muestra y los objetivos del estudio. Cuando se dispone de datos que cumplen con los supuestos de normalidad y homogeneidad de varianzas, las pruebas paramétricas son generalmente la opción preferida debido a su mayor poder estadístico. Por ejemplo, en un estudio clínico que mide la presión arterial de dos grupos de pacientes, si los datos son normalmente distribuidos, se podría usar una prueba t para comparar los grupos.

En contraste, si los datos están sesgados o no distribuidos normalmente, sería más apropiado utilizar pruebas no paramétricas. Imaginemos un escenario en el que se desea comparar la satisfacción del cliente entre varios grupos de consumidores utilizando una escala de Likert. En este caso, dado que los datos son ordinales, una prueba de Kruskal-Wallis podría ser más adecuada para estos datos. Además, cuando se trabaja con tamaños de muestra pequeños, las pruebas no paramétricas pueden ser más apropiadas incluso si los datos admiten análisis paramétricos.

Consideraciones al elegir entre pruebas paramétricas y no paramétricas

Al momento de elegir entre pruebas paramétricas y no paramétricas, los investigadores deben considerar varios factores. El primero y más importante es evaluar las características de los datos. Si los datos cumplen con los supuestos de la prueba paramétrica, es recomendable utilizarla debido a su mayor potencia. Sin embargo, si hay dudas sobre la normalidad o los datos incluyen observaciones extremas, las pruebas no paramétricas son una alternativa válida.

Otro factor importante es el tamaño de la muestra. En general, las pruebas paramétricas pueden funcionar mejor con muestras más grandes, donde los supuestos son más fáciles de cumplir a través del Teorema Central del Límite. Por otro lado, las pruebas no paramétricas son útiles incluso con tamaños de muestra pequeños. Además, los objetivos de investigación juegan un papel crucial; si los investigadores están interesados en la magnitud del efecto y en estimaciones precisas, las pruebas paramétricas pueden ser más informativas, mientras que las pruebas no paramétricas pueden ser adecuadas en situaciones de exploración inicial o cuando se manejan datos ordinales.

Conclusiones

Las pruebas paramétricas y no paramétricas son herramientas fundamentales en el análisis estadístico que permiten a los investigadores tomar decisiones bien fundamentadas. Cada tipo de prueba tiene su propio conjunto de supuestos, ventajas y limitaciones. Las pruebas paramétricas son potentes y útiles cuando se cumple con la normalidad y la homogeneidad de varianzas, mientras que las pruebas no paramétricas ofrecen versatilidad y aplicabilidad cuando se manejan datos que no cumplen con esos supuestos o en situaciones donde se requiere análisis de datos ordinales. Finalmente, la elección entre estas pruebas debe hacerse cuidadosamente, teniendo en cuenta la naturaleza de los datos, el tamaño de la muestra y los objetivos de la investigación. Con una comprensión clara de estas pruebas, los investigadores pueden aplicar las mejores prácticas en su análisis de datos y garantizar que sus conclusiones sean válidas y confiables.

Si quieres conocer otros artículos parecidos a Qué son las pruebas paramétricas y no paramétricas puedes visitar la categoría Estadística.