La regularización en modelos estadísticos y su importancia

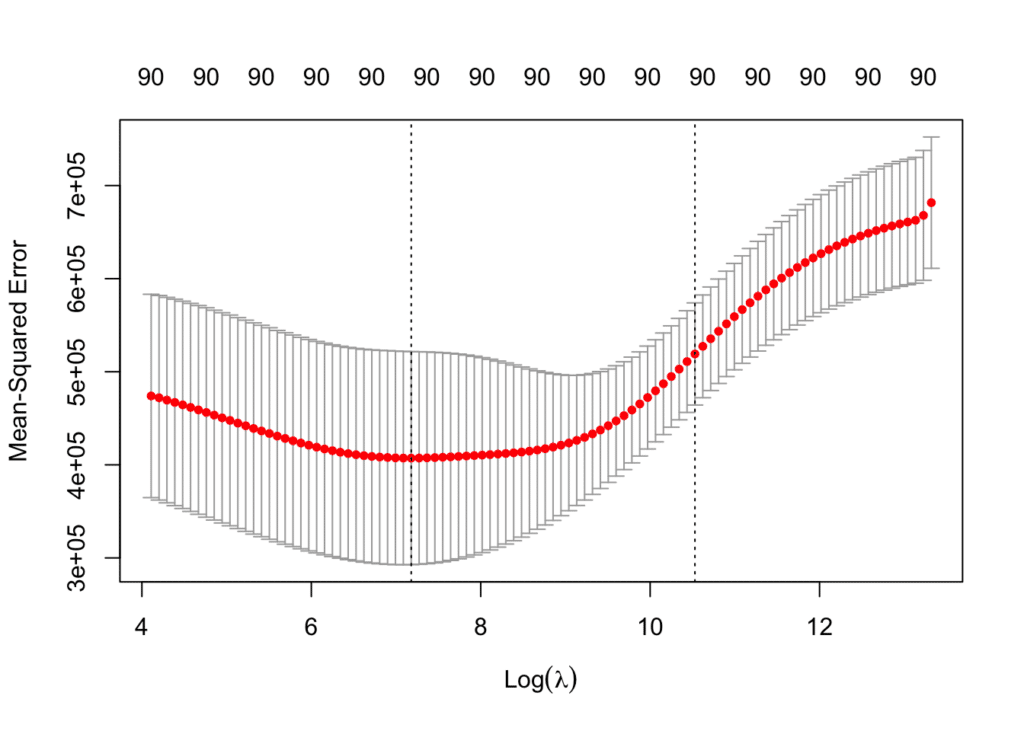
En el ámbito de la estadística y el aprendizaje automático, la regularización ha emergido como una técnica crucial que ayuda a prevenir el sobreajuste y a mejorar la generalización de los modelos predictivos. A medida que los conjuntos de datos se vuelven más complejos y variados, la necesidad de métodos que optimicen el rendimiento se vuelve aún más acuciante. La regularización no solo aborda el problema de la complejidad excesiva de los modelos, sino que también proporciona un camino hacia una interpretación más robusta y válida de los resultados, asegurando que los modelos se comporten adecuadamente en datos no vistos.

Este artículo se sumerge en el fascinante mundo de la regularización en modelos estadísticos, explorando sus fundamentos, métodos más comunes, aplicaciones y la importancia crítica que tiene en la ciencia de datos contemporánea. A medida que avanzamos, se discutirá cómo la regularización no solo fortalece la capacidad predictiva, sino que también permite una mejor interpretación de las relaciones subyacentes dentro de los datos. Al final de este artículo, los lectores tendrán una comprensión clara de por qué la regularización se considera una piedra angular en el desarrollo de modelos estadísticos avanzados.

¿Qué es la regularización en modelos estadísticos?

La **regularización** se refiere a un conjunto de técnicas utilizadas para restringir o modificar un modelo con el propósito de prevenir el sobreajuste. El sobreajuste ocurre cuando un modelo se ajusta demasiado a los datos de entrenamiento, capturando el ruido en lugar de la tendencia subyacente. Este fenómeno puede resultar en un rendimiento deficiente al aplicarse a nuevos conjuntos de datos. Por tanto, la regularización se convierte en un mecanismo poderoso para mejorar la capacidad general del modelo.

La idea fundamental detrás de la regularización es introducir una penalización en la función de costo que el modelo intenta minimizar durante el entrenamiento. Al hacer esto, se busca enfocar la atención del algoritmo en encontrar soluciones que no solo minimicen el error de entrenamiento, sino que también sean más simples y robustas. Dos de las formas más comunes de regularización son Lasso y Ridge, que se explican en detalle en las secciones posteriores.

Tipos de regularización: Lasso y Ridge

Existen diversas técnicas de regularización, pero los métodos más populares son la **regularización L1 (Lasso)** y la **regularización L2 (Ridge)**. La principal diferencia entre las dos radica en la forma de penalizar los coeficientes del modelo. En la regularización Lasso, se añade una penalización que es proporcional al valor absoluto de los coeficientes. Esto no solo tiende a reducir algunos de los coeficientes a cero, lo que fomenta una **selección de características** efectiva, sino que también proporciona un modelo interpretativo y menos complejo.

La regularización Ridge, por otro lado, penaliza los coeficientes al elevar al cuadrado sus valores. Este método tiende a reducir el tamaño de todos los coeficientes, más que llevar algunos a cero. Como resultado, los modelos entrenados con regularización Ridge mantienen todas las características, pero con coeficientes más pequeños. Esta técnica es particularmente útil cuando se tienen muchas características colineales, ya que ayuda a estabilizar la estimación de los coeficientes.

Aplicaciones de la regularización en diversos campos

La **regularización** tiene aplicaciones en un amplio rango de disciplinas, desde finanzas y biología hasta procesamiento de imágenes y reconocimiento de voz. En el campo financiero, los modelos predictivos que se ajustan a datos históricos pueden beneficiarse enormemente de la regularización al evitar que el ruido de las transacciones no relevantes afecte la predicción futura. Por ejemplo, la regularización se utiliza para predecir el riesgo de crédito, donde la capacidad de identificar características no relevantes es fundamental para tomar decisiones de préstamo acertadas.

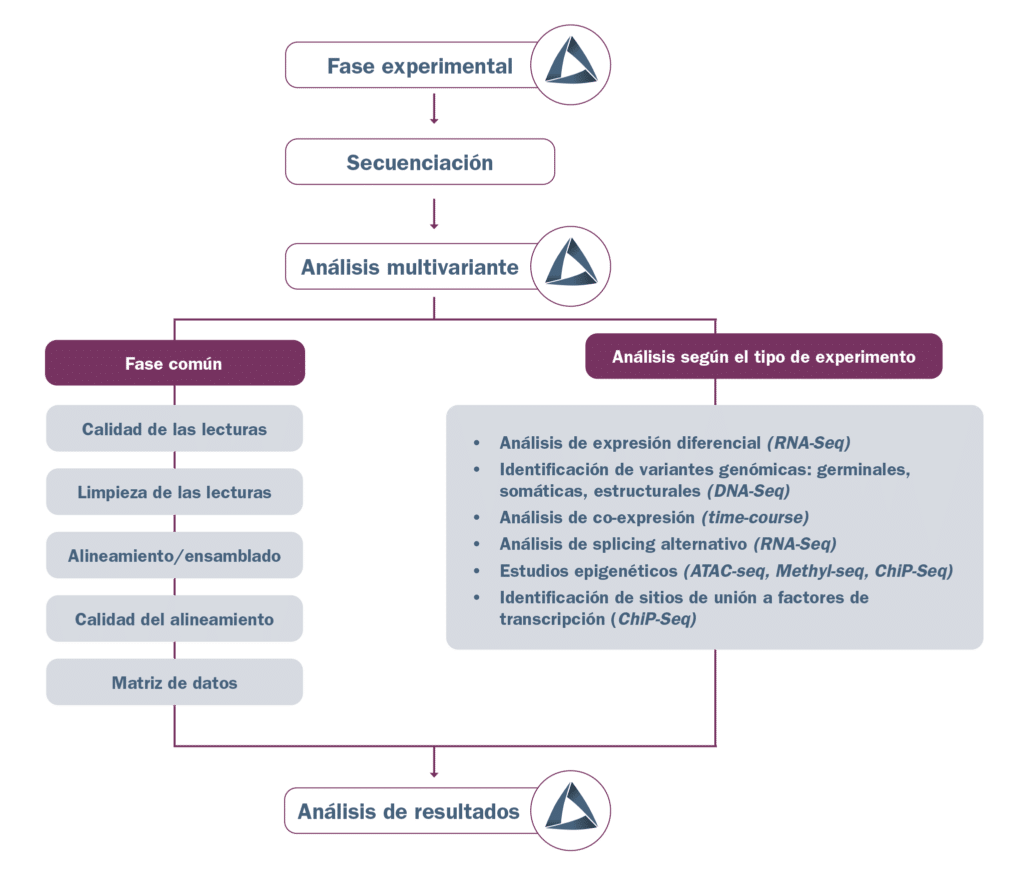
En biología, la regularización ayuda a modelar las complejas interacciones biológicas en estudios genómicos, donde puede haber un número muy alto de variables en comparación con el número de observaciones. La regularización permite seleccionar genes significativos que pueden estar vinculados a ciertas enfermedades, ayudando así a los investigadores a enfocar su atención en los factores con mayor relevancia. Además, en el procesamiento de imágenes, la regularización se implementa para mejorar la calidad de las reconstrucciones de imagen al garantizar que el modelo no se vea influenciado por artefactos o ruido en los datos de entrada.

Beneficios de la regularización en la modelización estadística

Los beneficios de implementar **regularización** en modelos estadísticos son múltiples y notables. En primer lugar, permite a los modelos ser menos susceptibles al sobreajuste, lo cual es crítico en un contexto donde la generalización es esencial. Este enfoque no solo mejora la precisión del modelo, sino que también proporciona una mayor confianza en los resultados que se obtienen. En segundo lugar, la regularización potencia la interpretabilidad de los modelos, ya que tiende a reducir la complejidad y enfocar la atención en las variables más significativas. Esto podría cambiar la forma en que los analistas y científicos de datos comunican las conclusiones, haciendo que los resultados sean accesibles incluso para audiencias no técnicas.

Además, la regularización puede ahorrar tiempo y recursos durante la fase de modelización. Al centrarse en un subconjunto reducido de características relevantes, se puede optimizar el proceso de análisis, evitando la necesidad de interpretar y manejar grandes volúmenes de datos innecesarios. Esto es particularmente importante en la era de grandes datos, donde la cantidad de información puede ser abrumadora. La regularización proporciona un marco claro que permite a los analistas tomar decisiones fundamentadas en torno a qué variables mantener en sus modelos finales.

Desafíos de la regularización

A pesar de sus múltiples beneficios, la regularización también presenta ciertos desafíos. Uno de los principales problemas radica en la selección de parámetros de regularización adecuados. La elección de la fuerza de la penalización, por ejemplo, puede ser crítica y, si se selecciona incorrectamente, puede conducir a un modelo subóptimo. Esto requiere de un proceso de validación cuidadosa, que puede resultar tedioso y laborioso.

Otro desafío es que no todos los algoritmos de aprendizaje automático se pueden regularizar de manera efectiva. Algunos modelos son inherentemente susceptibles al sobreajuste, mientras que otros pueden no beneficiarse de la regularización de la misma manera. Por lo tanto, es crucial que los investigadores y profesionales comprenden cómo interactúan sus modelos con las técnicas de regularización que elijan.

Conclusión

La **regularización** es una técnica fundamental en el ámbito de la modelización estadística que ayuda a garantizar la generalización y la robustez de los modelos. A través de métodos como Lasso y Ridge, se puede reducir el riesgo de sobreajuste, mejorar la interpretabilidad y optimizar el rendimiento del modelo en contextos diversos. A pesar de los desafíos que presenta, los beneficios de la regularización superan claramente sus inconvenientes, convirtiéndola en una herramienta esencial para cualquier aspirante a científico de datos o estadístico. En un campo que está en constante evolución, comprender y aplicar técnicas de regularización se convierte en un aspecto imprescindible para lograr resultados confiables y significativos en cualquier análisis de datos.

Si quieres conocer otros artículos parecidos a La regularización en modelos estadísticos y su importancia puedes visitar la categoría Estadística.