Análisis univariado: definición, utilidad y aplicaciones estadísticas

El análisis univariado es una técnica fundamental en el campo de la estadística que permite examinar y describir un solo conjunto de datos. A través de este análisis, los estadísticos pueden obtener información valiosa sobre la distribución, tendencia central y dispersión de datos individuales, contribuyendo así a una mejor comprensión de fenómenos y comportamientos en una variedad de campos, como la economía, la psicología y la salud pública. Esta herramienta es crucial no solo para los investigadores, sino también para los profesionales que buscan interpretar datos de manera efectiva.

En este artículo, profundizaremos en el concepto de análisis univariado, su relevancia en el mundo de la estadística y las diferentes metodologías y aplicaciones. A medida que avancemos, exploraremos diversas formas de llevar a cabo este análisis y cómo cada enfoque puede proporcionar conocimientos únicos sobre los datos. Tanto si eres un estudiante que da sus primeros pasos en el análisis de datos como si eres un profesional experimentado, entender cómo aplicar el análisis univariado te ayudará a realizar inferencias significativas y tomar decisiones informadas basadas en tus datos.

¿Qué es el análisis univariado?

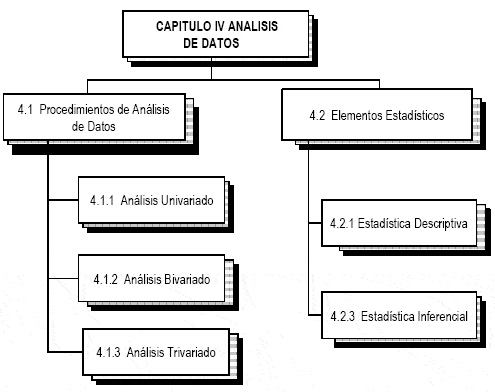
El análisis univariado se define como el examen de un solo variable en un conjunto de datos. Este tipo de análisis es el más simple de todos los análisis estadísticos, ya que no tiene en cuenta interacciones entre múltiples variables; en lugar de eso, se centra en una única dimensión a la vez. Por lo general, el análisis univariado implica la creación de resúmenes estadísticos, visualizaciones y gráficos que facilitan la comprensión de la variable en cuestión. Los métodos incluyen medidas como la media, la mediana, la moda, el rango y la desviación estándar, entre otros.

Una de las primeras cosas que se realizan en un análisis univariado es la creación de un perfil descriptivo de la variable. Esto puede incluir la identificación del tipo de variable (cualitativa o cuantitativa), así como la determinación de la escala de medición (nominal, ordinal, intervalar o de razón). Entender la naturaleza de la variable es fundamental, ya que influye en las técnicas de análisis que se pueden utilizar. Por ejemplo, para una variable categórica, se podrían utilizar tablas de frecuencia y gráficos de barras, mientras que para una variable continua, se podría preferir un histograma o un boxplot.

Utilidad del análisis univariado

El análisis univariado tiene múltiples aplicaciones, y su utilidad radica en su capacidad para proporcionar un marco claro y conciso para entender un conjunto de datos específico. En términos de utilidad, este tipo de análisis permite a los investigadores y estadísticos detectar patrones, identificar anomalías y resumir datos de manera efectiva. Por ejemplo, en el ámbito de la salud pública, un análisis univariado puede ayudar a entender la prevalencia de una enfermedad en una población al observar la distribución de una variable como la edad.

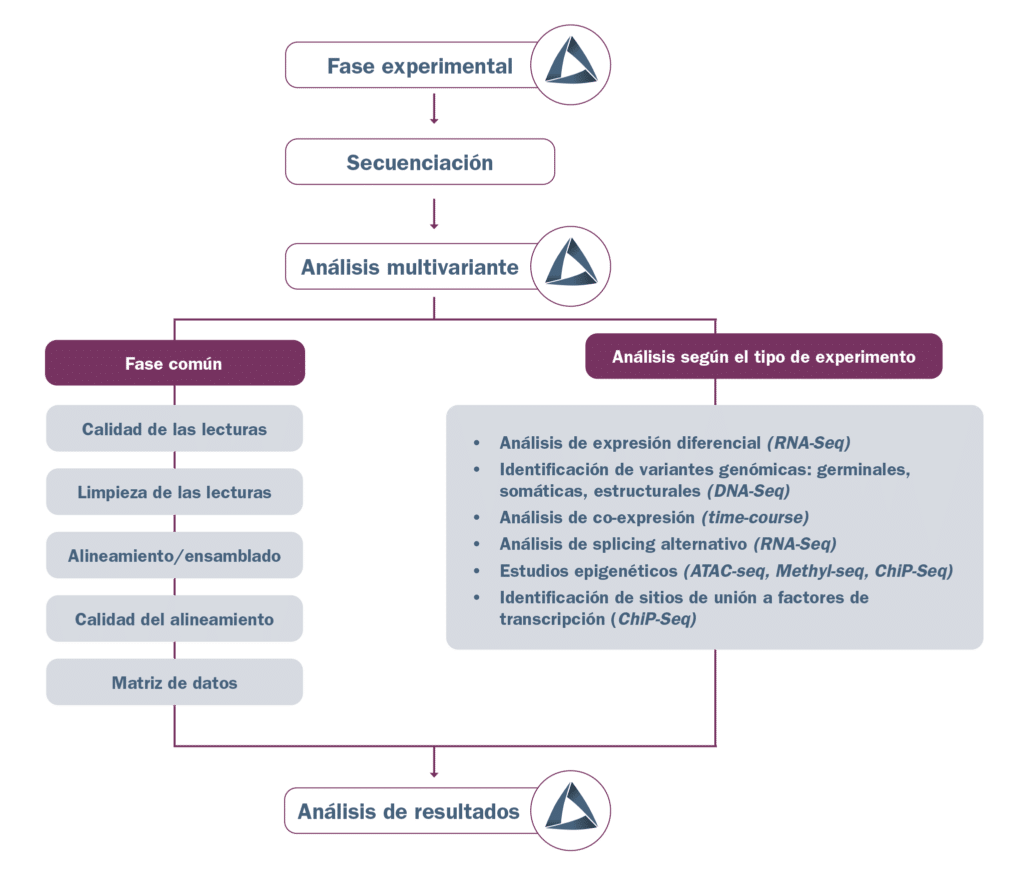
Además, el análisis univariado es crucial en las etapas iniciales de cualquier análisis de datos, ya que proporciona una visión general que puede influir en las decisiones futuras sobre el tipo de análisis multivariado que se debe realizar. Identificar la naturaleza de la variable y su distribución puede ayudar a determinar si se requiere una transformación de los datos o si hay valores atípicos que necesitan ser manejados antes de considerar análisis más complejos. Esta etapa es esencial para asegurar la validez de los resultados en sus análisis posteriores.

Métodos y técnicas del análisis univariado

Existen diversas **técnicas** para llevar a cabo el análisis univariado, y cada una tiene su utilidad específica según el tipo de variable y el objetivo del estudio. Entre las técnicas más utilizadas se encuentran las siguientes:

Una de las técnicas más comunes es la gráfica de histogramas, que permite visualizar la distribución de una variable continua dividiendo los datos en intervalos y contando el número de observaciones en cada intervalo. Esta visualización es fundamental para identificar la forma de la distribución (normal, sesgada, etc.) y detectar potenciales outliers o valores atípicos.

Otra herramienta importante es el boxplot o gráfico de caja, que agrega medidas descriptivas, tales como la mediana, los cuartiles y los valores atípicos. El boxplot es especialmente útil para ofrecer una visión más clara de la dispersión y los valores atípicos de los datos, comparando diferentes grupos de una manera eficiente.

En el caso de variables categóricas, se utilizan tablas de frecuencia y gráficos de barras para ilustrar la distribución de la variable. Estos gráficos permiten visualizar de forma rápida y efectiva la cantidad de observaciones en cada categoría, lo que facilita la identificación de cualquier tendencia o patrón en los datos.

Aplicaciones del análisis univariado

El análisis univariado se aplica en diversas disciplinas, desde las ciencias sociales hasta la economía y la biología. En el campo de la psicología, por ejemplo, se utiliza para examinar una sola característica de los encuestados, como la satisfacción laboral, a través de escalas de medición y gráficos que muestran la distribución de respuestas. Este tipo de análisis puede informar a los profesionales sobre la salud mental de una población y ayudar a diseñar intervenciones adecuadas.

En el ámbito empresarial, el análisis univariado puede servir para entender el comportamiento del consumidor al estudiar una variable como el gasto mensual. Al analizar esta variable, las empresas pueden identificar patrones que les permiten segmentar su mercado y dirigir mejor sus estrategias de marketing. Por ejemplo, pueden compararse las tendencias de gasto entre diferentes grupos de edad o ubicación geográfica, y así adaptar sus ofertas según las preferencias de cada segmento.

En estudios médicos, el análisis univariado también juega un papel crucial. Se usa para evaluar variables como la presión arterial, el colesterol y otros indicadores de salud en poblaciones para identificar tendencias y correlaciones que pueden indicar problemas de salud emergentes. Este tipo de análisis puede ayudar a las autoridades de salud pública a tomar decisiones informadas sobre recursos y estrategias de prevención.

Limitaciones del análisis univariado

A pesar de su utilidad, el análisis univariado presenta ciertas limitaciones que es crucial tener en cuenta. Al centrarse en una sola variable, este análisis puede ofrecer una visión incompleta del fenómeno que se estudia. No se puede captar la complejidad de las relaciones entre varias variables, lo que podría ser esencial para obtener una imagen más completa de la realidad. Por ejemplo, un análisis univariado sobre el ingreso familiar podría no ser suficiente para comprender cómo influyen otros factores, como la educación o el lugar de residencia.

Además, el análisis univariado puede ser engañoso si no se tiene en cuenta el contexto en el que se recogen los datos. Sin una comprensión del sesgo de muestreo o de las condiciones en las que se han recopilado los datos, las decisiones basadas exclusivamente en un análisis univariado pueden estar mal dirigidas o ser ineficaces. Por esta razón, es importante considerar el uso de análisis multivariados complementarios para enriquecer y validar los hallazgos obtenidos a partir de un análisis univariado.

Conclusión

El análisis univariado es una herramienta valiosa en la estadística que permite la evaluación y comprensión de una sola variable a partir de datos numéricos o categóricos. A través de diversas técnicas y visualizaciones, este análisis no solo proporciona información descriptiva esencial, sino que también ayuda a detectar patrones, anomalías y tendencias que pueden informar decisiones y estrategias futuras. Sin embargo, es importante recordar que, aunque el análisis univariado es fundamental, no debe ser utilizado de manera aislada. Comprender su contexto y complementarlo con análisis más complejos garantizará la precisión y relevancia de los resultados obtenidos. En última instancia, el dominio del análisis univariado prepara el camino para un análisis más profundo y sofisticado, ayudando a transformar los datos en información significativa.

Si quieres conocer otros artículos parecidos a Análisis univariado: definición, utilidad y aplicaciones estadísticas puedes visitar la categoría Estadística.