Uso de Curvas ROC en Bioinformática para Evaluar Modelos

En el mundo actual de la bioinformática, la evaluación y validación de modelos predictivos es esencial para obtener resultados precisos y útiles que puedan transformar el conocimiento biomédico y clínico. Las curvas ROC (Receiver Operating Characteristic) se han convertido en una herramienta fundamental en este contexto, permitiendo a los investigadores y científicos analizar cómo un modelo predice la presencia o ausencia de un fenómeno específico, ya sea una enfermedad, un marcador genético u otra variable de interés en biología. Con el desarrollo constante de técnicas de análisis de datos y aprendizaje automático, tener a la disposición una forma confiable de evaluar estos modelos es más crucial que nunca.

Este artículo se adentrará en la utilización de las curvas ROC en el campo de la bioinformática, explorando qué son, cómo se construyen y cómo interpretarlas en el contexto de la evaluación de modelos. Además, se discutirá su relevancia dentro de la investigación biomédica y cómo estas curvas pueden guiar a los científicos en la elección de los mejores modelos predictivos. A medida que avancemos en este tema, proporcionaremos ejemplos prácticos y casos de uso que destacarán la importancia de las curvas ROC en la investigación y desarrollo en bioinformática.

¿Qué son las Curvas ROC?

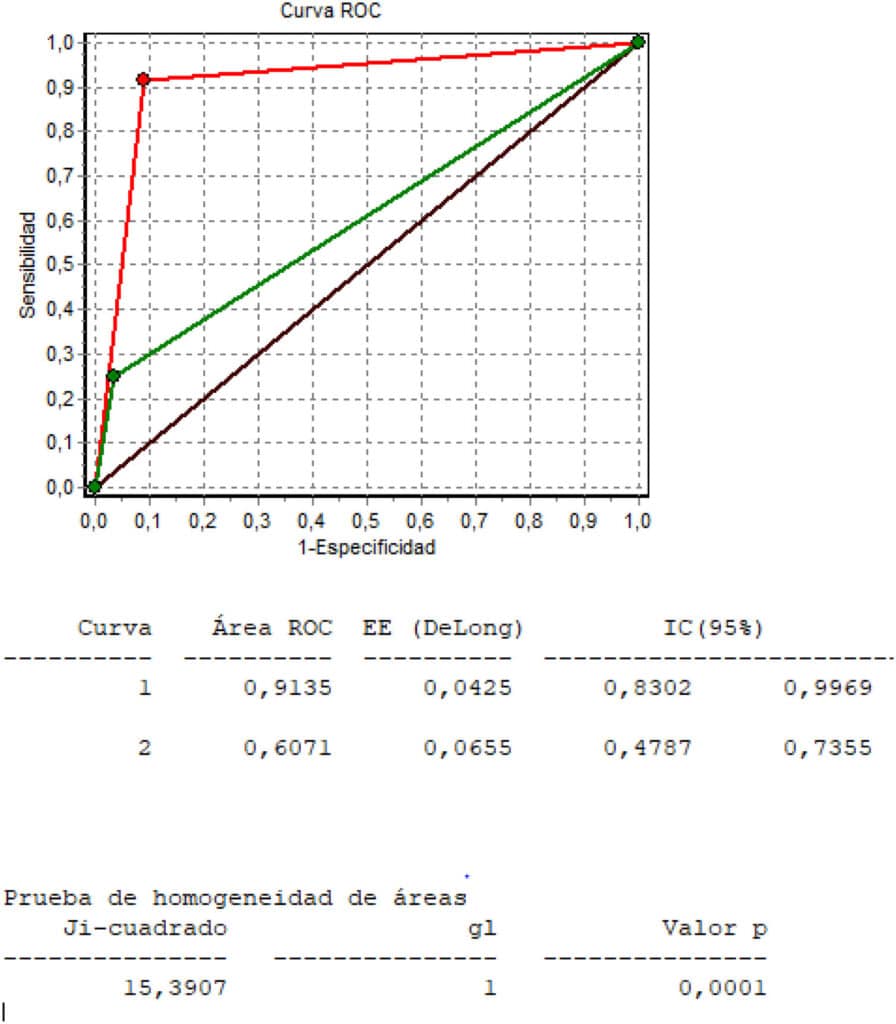
Las curvas ROC son representaciones gráficas que permiten visualizar el rendimiento de un modelo de clasificación a través de distintos umbrales de decisión. En términos más técnicos, estas curvas trazan la tasa de verdaderos positivos (sensibilidad) contra la tasa de falsos positivos (1 - especificidad) en varios puntos de umbral. Este enfoque permite a los investigadores discernir no solo la capacidad predictiva de un modelo, sino también cómo su performance varía con diferentes criterios de decisión.

El eje X de la curva representa la tasa de falsos positivos, mientras que el eje Y muestra la tasa de verdaderos positivos. Cuanto más cerca esté la curva del punto (0, 1), mejor será el rendimiento del modelo. Esto se debe a que un modelo ideal tendría una sensibilidad del 100% y una tasa de falsos positivos de 0%, lo que se traduce en un área bajo la curva (AUC) de 1. Por otro lado, si el modelo no tiene capacidad de discriminación, la AUC será de 0.5, indicativa de un rendimiento equivalente a la aleatoriedad.

Construcción de Curvas ROC

La construcción de una curva ROC a partir de datos requiere varios pasos importantes. En primer lugar, es necesario tener un conjunto de datos en el cual se disponga de una variable de respuesta y al menos una variable predictora. Luego, se entrena un modelo predictivo utilizando, por ejemplo, técnicas de regresión logística, redes neuronales, o métodos de aprendizaje automático, con el objetivo de clasificar los casos en positivos y negativos en función de la variable de respuesta.

Una vez que se cuenta con el modelo entrenado, se aplican los siguientes pasos: primero, se generan predicciones para el conjunto de datos utilizando el modelo. Luego, se calculan las tasas de verdaderos y falsos positivos ajustando el umbral de decisión que determina qué casos son clasificados como positivos. Este proceso se repite variando el umbral, lo que permite obtener una serie de puntos que serán utilizados para construir la curva.

Finalmente, la representación gráfica permite visualizar la relación entre estas tasas, donde cada punto en la curva corresponde a un umbral diferente. Esto no solo facilita detectar el punto óptimo que equilibra sensibilidad y especificidad, sino que también proporciona una manera intuitiva de evaluar el trade-off inherente a decisiones de diagnóstico en el ámbito clínico.

Interpretación de las Curvas ROC

La interpretación de las curvas ROC va más allá de simplemente observar la forma de la curva. Un aspecto clave es el cálculo del área bajo la curva (AUC). Como mencionamos anteriormente, este valor oscila entre 0 y 1, donde 1 indica un modelo perfecto y 0.5 indica un desempeño ineficaz. No obstante, AUC no es completamente infalible; debe complementarse con otras métricas de evaluación para obtener una visión holística del rendimiento del modelo.

A medida que se analiza la curva, es importante considerar el contexto del problema. Por ejemplo, en situaciones donde las consecuencias de falsos positivos son críticas (como en el diagnóstico de cáncer), podría ser deseable un modelo que minimice estas tasas incluso si ello implica un costo en la sensibilidad. Del mismo modo, en escenarios donde se podrían perder oportunidades valiosas por unión a un falso negativo, podría preferirse un modelo que priorice la sensibilidad.

Aplicaciones de las Curvas ROC en Bioinformática

Las aplicaciones de las curvas ROC en bioinformática son diversas y abarcan múltiples áreas de investigación. En el contexto de la epidemiología y la genómica, por ejemplo, se utilizan para evaluar la precisión de los modelos que identifican biomarcadores asociados a enfermedades. En estos estudios, es crítico diferenciar entre individuos sanos y aquellos con patologías a partir de datos moleculares complejos, donde las curvas ROC proporcionan un marco robusto para validar los modelos generados.

Otra aplicación notable de las curvas ROC es la comparación de múltiples modelos predictivos. Los investigadores a menudo desarrollan diferentes algoritmos para abordar un mismo problema y las curvas ROC ofrecen una metodología gráfica y cuantitativa que permite contrastar su desempeño. Al hacerlo, es posible identificar cuál de estos modelos tiene un mejor potencial para ser implementado en la práctica clínica o investigativa.

Además, las curvas ROC pueden emplearse a lo largo del proceso de descubrimiento de modelos, ayudando en la selección de características y minimizando la sobreajuste. Esto resulta crucial, especialmente en bioinformática, donde los conjuntos de datos pueden ser extensos y complejos, y tener herramientas que evalúen la calidad predictiva de un modelo en cada fase de desarrollo es esencial para alcanzar resultados confiables.

Limitaciones de las Curvas ROC

A pesar de ser una herramienta extremadamente valiosa, las curvas ROC no están exentas de limitaciones. Uno de los principales inconvenientes es que la AUC no refleja el rendimiento del modelo en la vida real en todos los contextos. En situaciones donde la prevalencia de la enfermedad es baja, un modelo con una alta AUC podría aún generar un número sustancial de falsos positivos, lo que puede tener implicaciones prácticas significativas.

Asimismo, las curvas ROC en sí mismas no ofrecen claridad sobre la probabilidad posterior de un evento o la proporción de casos positivos reales entre los positivos predichos. Es decir, a menudo se complementan con otras herramientas como la matriz de confusión y la curva PR (Precision-Recall), que pueden brindar un panorama más completo auto sobre el desempeño del modelo.

Reflexiones Finales sobre el Uso de Curvas ROC en Bioinformática

Las curvas ROC han demostrado ser una herramienta fundamental en la evaluación de modelos en el ámbito de la bioinformática, proporcionando una manera efectiva y visual de entender el rendimiento de los modelos de clasificación. A lo largo de este artículo, hemos explorado su construcción y referencia interpretativa, así como su amplia gama de aplicaciones en investigación y desarrollo.

El uso de las curvas ROC no solo ayuda en la validación de modelos, sino que también representa un paso crucial en el avance del conocimiento biomédico. Al ofrecer una forma estructurada de evaluar modelos predictivos, capacita a los investigadores a tomar decisiones informadas que pueden tener un impacto significativo en la medicina personalizada y el descubrimiento científico. A medida que el campo de la bioinformática sigue evolucionando, es probable que las técnicas de evaluación como las curvas ROC se mantengan en el centro de este proceso, guiando a los científicos hacia resultados más precisos y efectivas.

Si quieres conocer otros artículos parecidos a Uso de Curvas ROC en Bioinformática para Evaluar Modelos puedes visitar la categoría Estadística.