Uso de diagramas de dispersión en análisis de datos

El análisis de datos se ha convertido en una herramienta esencial en la era digital actual, donde la información fluye a un ritmo sin precedentes. En este contexto, los diagramas de dispersión han emergido como un recurso crucial para visualizar relaciones entre variables, permitiendo a los analistas e investigadores identificar patrones, tendencias y correlaciones que podrían no ser evidentes a simple vista. Estos diagramas, que muestran la distribución de datos en un plano cartesiano, ofrecen una perspectiva clara de cómo interactúan diferentes conjuntos de datos, ofreciendo así valiosas intuiciones en diversas disciplinas.

Este artículo se adentrará en el fascinante mundo del uso de los diagramas de dispersión en el análisis de datos. Exploraremos su funcionalidad, cómo se pueden integrar en procedimientos analíticos, y cuál es su importancia en la interpretación de resultados. Además, discutiremos ejemplos prácticos y abordaremos aspectos técnicos que son vitales para su correcta aplicación. Al final, se espera proporcionar un entendimiento sólido sobre por qué estos diagramas son imprescindibles en el análisis moderno de datos.

¿Qué son los diagramas de dispersión?

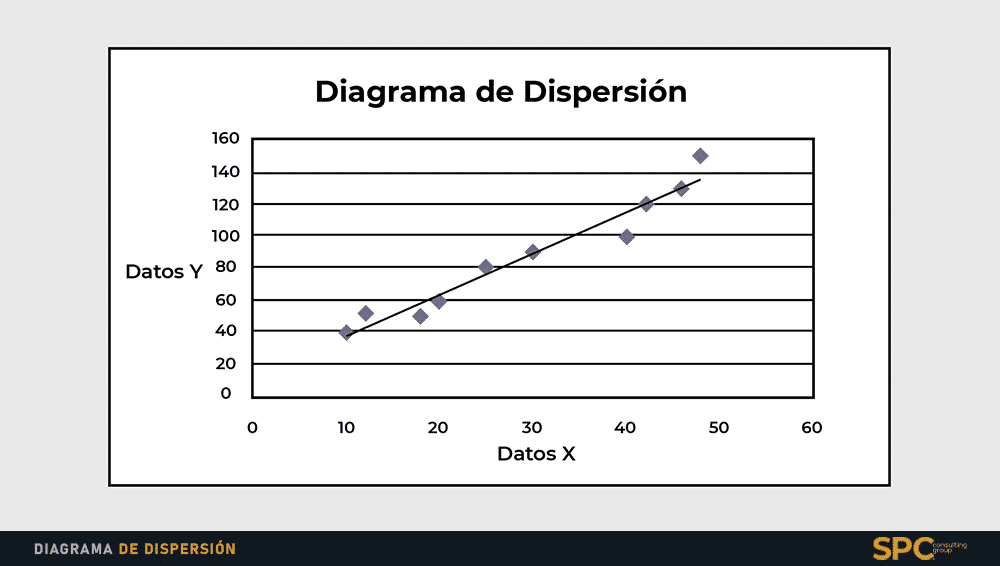
Un diagrama de dispersión es una representación gráfica que muestra la relación entre dos o más variables. Se utiliza para visualizar la distribución de puntos de datos en un plano, donde cada punto representa la unión de valores de estas variables. Las variables típicamente se colocan en los ejes X (horizontal) e Y (vertical), lo que permite observar cómo una variable podría influir o estar relacionada con la otra.

Este tipo de gráfico es especialmente útil cuando se desea observar la correlación. Por ejemplo, en estudios donde se analiza el impacto de la publicidad en las ventas, un diagrama de dispersión puede ayudar a visualizar si un incremento en la inversión publicitaria se traduce en un aumento en las ventas, indicando una posible relación positiva.

Tipos de relaciones que se pueden observar

Los diagramas de dispersión son capaces de mostrar diferentes tipos de relaciones entre variables que pueden clasificarse generalmente en tres categorías: lineales, no lineales y ninguna relación. Cuando observamos una relación lineal, los puntos parecen alinearse a lo largo de una línea recta, lo que indica que al aumentar una variable, también lo hace la otra de manera predecible. Este tipo de relación es muy común en análisis estadísticos y sirve como base para muchas técnicas de regresión.

Por otro lado, una relación no lineal se presenta cuando los puntos de datos no siguen un patrón recto, sino que pueden formar curvas o formas más complejas. Estas relaciones a menudo requieren métodos de modelado más sofisticados, ya que los cambios en una variable podrían impactar a la otra de formas inesperadas. Por último, si no se observa ningún patrón claro entre los puntos, esto sugiere que no hay relación significativa entre las variables analizadas, lo que puede ser tan revelador como identificar una correlación.

Aplicaciones en diferentes campos

Los diagramas de dispersión encuentran aplicaciones en una amplia gama de campos. En el ámbito científico, se utilizan para experimentar con datos de laboratorio, donde los investigadores pueden observar cómo diferentes concentraciones de un compuesto químico afectan a una reacción específica. Esto no solo optimiza los resultados experimentales, sino que también economiza recursos al guiar el enfoque en variables relevantes.

En el mundo de los negocios, los analistas emplean estos diagramas para examinar la relación entre distintas métricas de desempeño, como el gasto en marketing y las ventas o la satisfacción del cliente frente a la retención. Este análisis permite formular estrategias más efectivas basadas en las evidencias obtenidas de los diagramas de dispersión.

Cómo crear un diagrama de dispersión

La creación de un diagrama de dispersión eficaz requiere varios pasos fundamentales. Primero, se necesita asegurar que los datos estén correctamente recolectados y organizados. Cada punto en el diagrama debe corresponder a un conjunto de valores para las dos variables que se están analizando. Esto implica la limpieza de datos, lo que garantiza que no haya valores atípicos que puedan distorsionar los resultados finales.

Una vez que los datos están listos, el siguiente paso es elegir la herramienta adecuada para crear el gráfico. Programas como Excel, Google Sheets o software estadístico avanzado como R y Python ofrecen funcionalidades que permiten crear diagramas de dispersión de forma sencilla y efectiva. También es importante etiquetar claramente cada eje, así como el título del gráfico, para que el lector pueda entender facilmente qué se está visualizando. Además, agregar notas sobre puntos específicos o incluir un apartado que explique la metodología puede enriquecer la presentación final, mitigando posibles confusiones para el observador.

Interpretación de un diagrama de dispersión

La interpretación de un diagrama de dispersión puede ser directa, pero siempre requiere un análisis cuidadoso. Observar la forma en que los puntos se distribuyen puede proporcionar información crucial sobre la relación entre las variables. En el caso de una relación lineal, se puede calcular la pendiente de la línea de ajuste para medir la fuerza y dirección de la relación. Asimismo, el coeficiente de correlación, que va de -1 a 1, puede ser de gran ayuda; un valor cercano a 1 indica una fuerte correlación positiva, mientras que valores cercanos a -1 sugieren una fuerte correlación negativa.

Es crucial también estar atento a los valores atípicos, que son puntos que no se alinean con el comportamiento general del resto de los datos. Estos pueden indicar información importante que no debe ser ignorada y que podría requerir un análisis más profundo para entender el fenómeno que subyace a ellos.

Limitaciones de los diagramas de dispersión

A pesar de ser una herramienta poderosa, los diagramas de dispersión tienen sus limitaciones. Uno de los principales inconvenientes es que solo visualizan la relación entre dos variables y, en muchos casos, las interacciones entre varias variables pueden ser complejas y multidimensionales. Esto puede resultar en que un diagrama de dispersión no capture todos los factores que influyen en la relación observada.

Adicionalmente, estas visualizaciones pueden llevar a interpretaciones erróneas si no se consideran contextos adicionales. Por ejemplo, una correlación podría existir debido a una variable oculta que afecta a ambas variables en análisis. Por lo tanto, es crucial complementar los diagramas de dispersión con análisis más complejos y otras herramientas estadísticas para obtener una visión más completa.

Conclusión

Los diagramas de dispersión son una herramienta esencial en el análisis de datos, permitiendo a los investigadores y analistas identificar y explorar relaciones entre variables de manera efectiva. Desde su aplicación en el ámbito científico hasta su relevancia en el análisis de métricas de negocio, su capacidad para resumir y presentar datos visualmente hace que sean de gran utilidad en la toma de decisiones. Sin embargo, como con cualquier herramienta, es necesario utilizarlos con precaución, comprensión y en combinación con otros métodos analíticos para garantizar una interpretación precisa y completa. En un mundo donde los datos continúan expandiéndose, el dominio de técnicas como los diagramas de dispersión será cada vez más valioso.

Si quieres conocer otros artículos parecidos a Uso de diagramas de dispersión en análisis de datos puedes visitar la categoría Estadística.